Chapter 2 Introduction
2.1 Models
- Models are a simplified representation of the world.
- Models consist of variables, relations, and parameters.
- Models’ interpretation and use are determined by the mindset.
2.1.1 Models Simplify Data
Every day, people use data for tasks such as predictions, automation, science, and making decisions:
- Identify patients prone to drug side effects.
- Find out how climate change affects bee hives.
- Predict which products will be out-of-stock.
Each data point has details to contribute:
- Patient with ID 124 got acne.
- Bee colony 27 shrank during the drought in 2018.
- On that one Tuesday the flour was sold out.
Data alone aren’t enough to solve these tasks. Data are noisy and high-dimensional – most of the information will be irrelevant for the task. No matter how long a human looks at the data, it’s difficult to impossible to gain insights just by sheer human willpower.
People rely on models to interpret and use data.
A model is a simplified representation of an aspect of the world.
Models learned from data – the focus of this book – glue together the raw data and the real world.
With a model, the modeler can make predictions, learn about the world, test theories, make decisions and communicate results to others.
2.1.2 Models Consist Of Variables And Learnable Functions
There is no philosophical consensus on the definition of a model. For our purpose, a mathematical model consists of variables and functions.
Variables represent aspects of the world, or the model:
- The blood pressure of a patient is represented with a numerical value.
- Images are represented as tensors of pixels.
- Variables can also represent abstract aspects like happiness.
- Cluster assignment represent a form of grouping.
- Latent model variables.
Variables have different names in different mindsets: Random variables, covariates, predictors, latent variables, features, target, outcome, … The names can reveal the role of a variable in a model: For example, the “target” or “dependent variable” is the variable that we want to predict.
The functions relate the variables to each other (Figure 2.1) (Weisberg 2012):
- A linear regression expresses one variable as a weighted sum of the other variables.
- In deep Q-learning, a form of reinforcement learning, the value of an action (variable) is a function of the state of the environment (variables).
- In clustering, the output is usually a function that takes as input the variables of the data point and returns its cluster (variable).
- The joint distribution of variables describes the occurrence of certain variable values in a probabilist sense.
- Causal models represent relations between variables in a directed acyclic graph that can be translated into conditional (in-)dependencies.
The functions range from simple (like \(Y = 5 \cdot X\)) to complex, like a deep neural network.
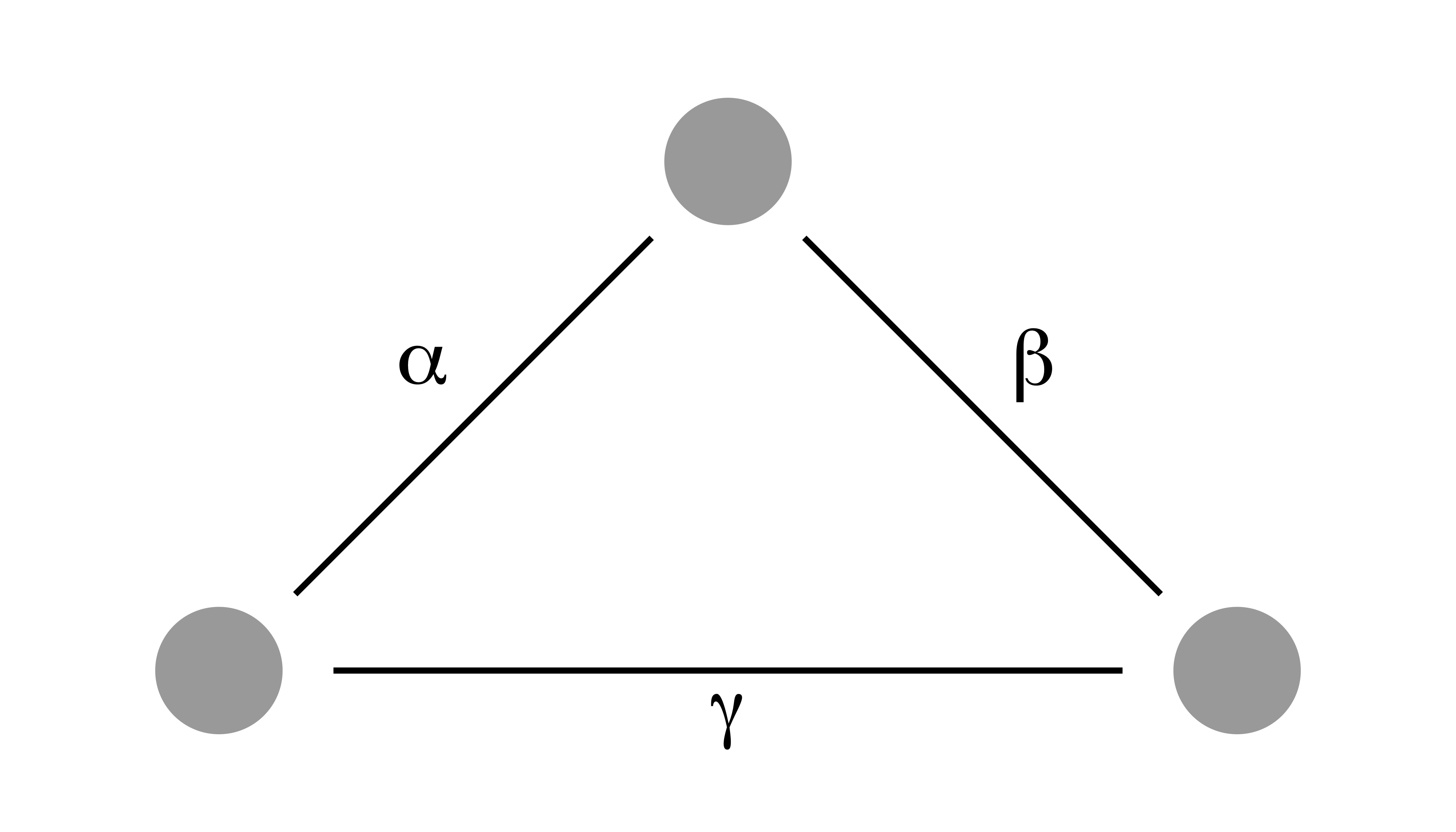
FIGURE 2.1: A mathematical model sets variables (dots) into relation (lines) using parameters.
2.1.3 From Data To Model
So far we have only discussed about variables and functions, the ingredients of a model, but not how they relate to data.
Modelers use data to find the best1 function to relate the variables. Depending on the mindset, the process of adapting a model’s function is called training, fitting or learning. In this process, the model function is optimized using data:
- In linear regression models, the weights in the sum are changed to minimized the squared difference between the weighted sum and the target variable.
- K-means clustering cycles between assigning data points to cluster centers and optimizing the centers to minimize distances.
The interpretation and use of the model can’t be derived from the model itself. Two mathematical identical models might be used in different ways, by different modelers. Models are children of the modeling mindsets they originated from.
2.2 Modeling Mindsets
- The same model can have different purposes in different mindsets.
- A mindset has strengths and limitations.
- Mindsets are cultural.
A model is a mathematical construct that doesn’t contain the purpose of the model. The purpose of the model – how to use and interpret it – depends on the modeling mindset. In order to derive knowledge about the world from the model, modelers need to make assumptions.
Consider a linear regression model that predicts regional rice yield as a function of rainfall, temperature, and fertilizer use: It’s a model, not a mindset:
- Can the modeler interpret the effect of fertilizer as causal to rice yield? Yes, if guided by a causal mindset.
- Is the model good enough for predicting rice yields? Depends if the modeler had a supervised learning mindset and evaluated the generalization error properly.
- Is the effect of fertilizer on yield significant? This requires a frequentist mindset.
2.2.1 A Mindset Is A Perspective Of The World
A modeling mindset is a specification of how to model the world using data (Figure 2.2. Modeling means investigating a real world phenomenon indirectly using a model. (Weisberg 2007) Modeling mindsets are like different lenses. All lenses show us the world, but with a different focus. Some lenses magnify things that are close, some that are far away. Some glasses are tinted so you can see in bright environments.
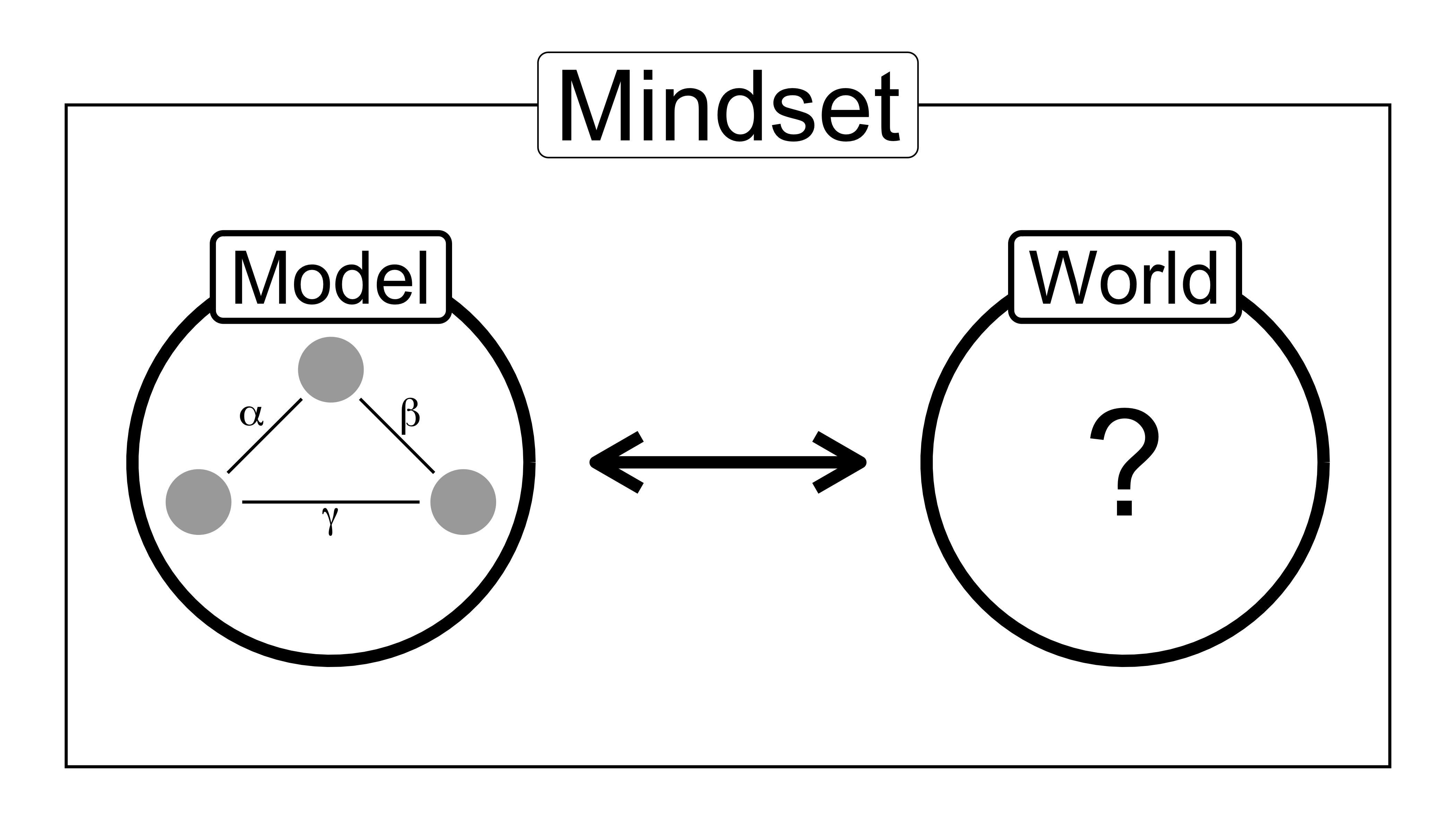
FIGURE 2.2: The real-world purpose of the model depends on the modeling mindset.
Modeling mindsets offer different lenses on the world. Mindsets differ in how they interpret probabilities – or whether probabilities are central to the mindset at all. While mindsets cover many different modeling tasks, they have some tasks where they really shine. Each mindset allows different questions, and so shapes how to view the world through the model. In supervised machine learning, for example, everything becomes a prediction or classification problem, while in Bayesian inference, the goal is to update our beliefs about the world using probability theory.
A modeling mindset limits the questions that can be asked. Some tasks are out of scope, because they don’t make sense in a particular modeling mindset. Supervised machine learners formulate tasks as prediction or classification problems. Questions about probability distributions are out of scope since the mindset is: choose the model that has the lowest generalization error given new data. So the best model could be any function, such as the average prediction of a random forest, a neural network, and a linear regression model. If the best model can be any function, questions that a statistician would normally ask (hypothesis testing, parameter estimation, …) is irrelevant, as the modeler can’t guarantee that the best model is a statistical model. Choosing a suboptimal model would violate the pure supervised learning mindset.
Each mindset has a different set of permissible models and ways to evaluate how good a model is. These sets may overlap – for example linear regression are both used in frequentist inference and supervised machine learning. But whether the linear regression is a good model for a given task is evaluated in different ways, as you will discover in the course of this book.
2.2.2 Modeling Mindsets Are Cultural
Modeling mindsets are not just theories; they shape communities and are shaped by people who model the world based on the mindset. In many scientific communities, the frequentist mindset is very common. I once consulted a medical student for his doctoral thesis. I helped him visualize some data. A few days later he came back, “I need p-values with this visualization.” His advisor told him that any data visualization needed p-values. His advisor’s advice was a bit extreme, and not advice that a real statistician would have given. However, it serves as a good example of how a community perpetuates a certain mindset. Likewise, if you were trying to publish a machine learning model in a journal that publishes mostly Bayesian analysis, I would wish you good luck. And I’d bet 100 bucks that the paper would be rejected.
The people within a shared mindset also accept the assumptions of that mindset. And these assumptions are usually not challenged, but mutually agreed upon. At least implicitly. In a team of Bayesians, whether or not to use priors won’t be challenged for every model. In machine learning competitions, the model with the lowest prediction error on new data wins. You will have a hard time arguing that your model should have won because it’s the only causal model. Modelers that find causality important, wouldn’t participate. Only modelers that have accepted the supervised learning mindset will thrive in such machine learning competitions.
2.2.3 Modeling Mindsets Are Archetypes
The modeling mindsets as I present them in this book are archetypes: pure and extreme forms of these mindsets. In reality, the boundaries between mindsets are much more fluid:
- A data scientist who primarily builds machine learning models might also use some simple regression models with hypothesis tests – without cross-validating the models’ generalization error.
- A research community could accept analyses that use both frequentist and Bayesian statistics.
- A machine learning competition could include a human jury who would award additional points if the model is interpretable and includes causal reasoning.
Have you ever met anyone who is really into supervised machine learning? The first question they ask is “Where is the labeled data?”. The supervised machine learner turns every problem into a prediction or classification problem. Or perhaps you’ve worked with a statistician who always wants to run hypothesis tests and regression models? Or you had intense discussion about probability with a hardcore Bayesian? Some people are walking archetypes of singular mindsets. But most people learned more than one mindset, and embraced bits of other mindsets. Most people’s mindset is already a mixture of multiple modeling mindsets. And that’s a good thing. Having an open mind about modeling ultimately makes you a better modeler.
References
What the best model is depends on the mindset.↩︎