Chapter 6 Likelihoodism – Likelihood As Evidence
- The likelihood is evidence for a statistical hypothesis (law of likelihood).
- Statistical hypotheses are compared by the ratio of their likelihoods.
- Likelihoodist ideas are used as well in frequentist and Bayesian statistics.
- A statistical modeling mindset with frequentism and Bayesianism as alternatives.
A frequentist, a Bayesian, and a likelihoodist walk into a wine bar. A sommelier quickly joins the three. The Bayesian wants to hear the sommelier’s opinion of the wines. The frequentist asks about the process: is the number of wines fixed or does it take until the first suitable wine? The likelihoodist ignores the sommelier and starts tasting the wines.
Frequentist inference has a long list of limitations. But it’s still the dominant statistical mindset in science and elsewhere. Bayesian analysis has seen a resurgence thanks to increased computational power for sampling from posteriors with MCMC. But using subjective prior probabilities doesn’t sit well with many statisticians. Could there be another way to “reform” the frequentist mindset? A mindset without the flawed hypothesis testing and without priors?
Likelihoodism is the purist among the statistical modeling mindsets: it fully embraces the likelihood function as evidence for a statistical hypothesis. Likelihoodism is an attempt to make statistics as objective as possible. It’s also impractical, as we will see. Nonetheless, the likelihoodist mindset offers a fresh perspective on Bayesian versus frequentist inference, and an interesting approach to comparing hypotheses about data.
6.1 Statistical Mindsets Use Likelihood Differently
The likelihood function links observed data to theoretic distributions. * Bayesians multiply prior distributions with the likelihood to get the posterior distributions of the parameters. * Frequentists use the likelihood to estimate parameters and construct “imagined” experiments that teach us about long-run frequencies (hypothesis tests and confidence intervals). * Likelihoodists view the likelihood as evidence derived from data for a statistical hypothesis. * Likelihoodists are likelihood-purists and therefore reject the non-likelihood elements from frequentism and Bayesianism: They reject priors because they are subjective; They reject the frequentists’ reliance on “imagined” experiments because these never-observed experiments violate the likelihood principle.
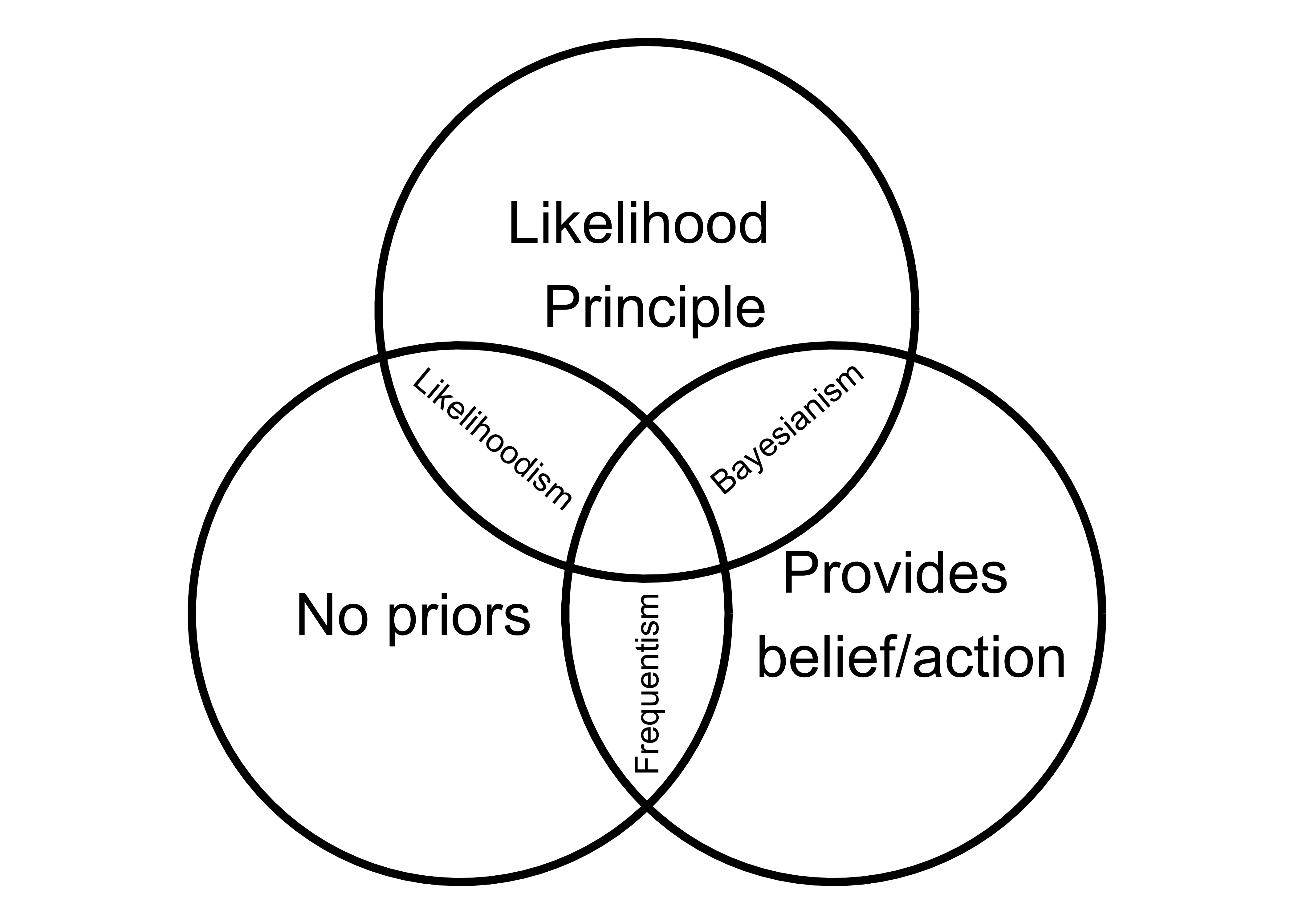
FIGURE 6.1: How Bayesianism, frequentism, and likelihoodism overlap and differ. Figure inspired by Greg Gandenberger: https://gandenberger.org/2014/07/28/intro-to-statistical-methods-2/.
Let’s take a look at the likelihood principle that is so central to the likelihoodist mindset.
6.2 Likelihood Principle
“The likelihood principle asserts that two observations that generate identical likelihood functions are equivalent as evidence.” (Richard 2017) As a consequence, all evidence that comes from the data about a quantity of interest such as a model parameter has to be part of the likelihood function. If we reverse the statement: The likelihood principle is violated if any information from the data enters the analysis outside of the likelihood. Both the Bayesian and the likelihoodist approaches adhere to the likelihood principle: All evidence from the data about the parameters is included in the likelihood. Bayesians use priors, but as long as they don’t include any information from the data, it’s fine. 6
Frequentists use hypothesis tests, confidence intervals and p-values. All of these require “imagined” experiments, including an assumption how these are distributed. An example where frequentism violates the likelihood principle through different stopping criteria for data collection.
Suppose a frequentist want to see if a coin is fair or if head comes up more often. The null hypothesis says that the coin is fair, the alternative hypothesis says that the coin produces more head tosses. The experiment has two variables: the number of heads, and the number of coin tosses. Imagine two experiments that produce the same data:
- Flip coin 12 times. Observe 9 heads.
- Flip the coin until tail appears 3 times. The third tail appears on the 12th flip.
Same outcome, different stopping criteria. Should both experiments come to the same conclusion about the fairness of the coin? Depends on the mindset.
- Both experiments have the same likelihood, up to a constant factor. Likelihoodists would say that both experiments carry the same evidence.
- Frequentists might use a hypothesis test with confidence level 5%. Since the experiments have different stopping criteria, the frequentist uses different tests. As a result, the frequentist would reject the null hypothesis in experiment 2), but would not reject it in experiment 1).
I’ll spare you the math behind this example. The coin flip scenario is not completely artificial: Imagine a domain expert asks a statistician to perform an analysis with 1000 data points. For the frequentist it matters whether the domain expert had a rule to stop after 1000 data points, or whether the expert would continue collecting data depending on the outcome of the analysis
For the likelihoodist, the stopping criterion doesn’t matter, because of the likelihood principle. But the likelihood principle alone isn’t sufficient to create a coherent modeling mindset, as it doesn’t offer guidance how to evaluate models. That’s what the law of likelihood is for.
6.3 Law of Likelihood
The law of likelihood allows the modeler to use the likelihood as evidence for a hypothesis. The law says (Hacking 1965):
If the likelihood for hypothesis A is larger than for hypothesis B, given some data, then the data counts as evidence that supports A over B, and the ratio of the likelihoods measures the strength of this evidence. Hypotheses A and B can be the same regression model, except that model B uses an additional variable. For example, model A predict diabetes from diet and model B from diet and age. Hypothesis A says that diabetes depends on diet, hypothesis B says that it depends on diet and age. Both models produce a likelihood score, which the modeler can compare. Thanks to the law of likelihood, the modeler may interpret the ratio of likelihoods as evidence.
Likelihoodists may use a rule of thumb for judging the strength of evidence. For example, a likelihood ratio of 8 is considered fairly strong and 32 or more is considered “strong favoring”.(Richard 2017)
Likelihoodists also use the likelihood ratio for describing the uncertainty of parameter estimates. Fitting a model produces a parameter estimate, which has the highest likelihood. Varying this parameter reduces the likelihood. How much less likely the varied value compared to the estimate is, can be judged by the likelihood ratio. The likelihood ratio can also produce likelihood intervals: The range of parameter values where the likelihood ratio remains below a specified threshold, compared to the estimate (see Figure 6.2.
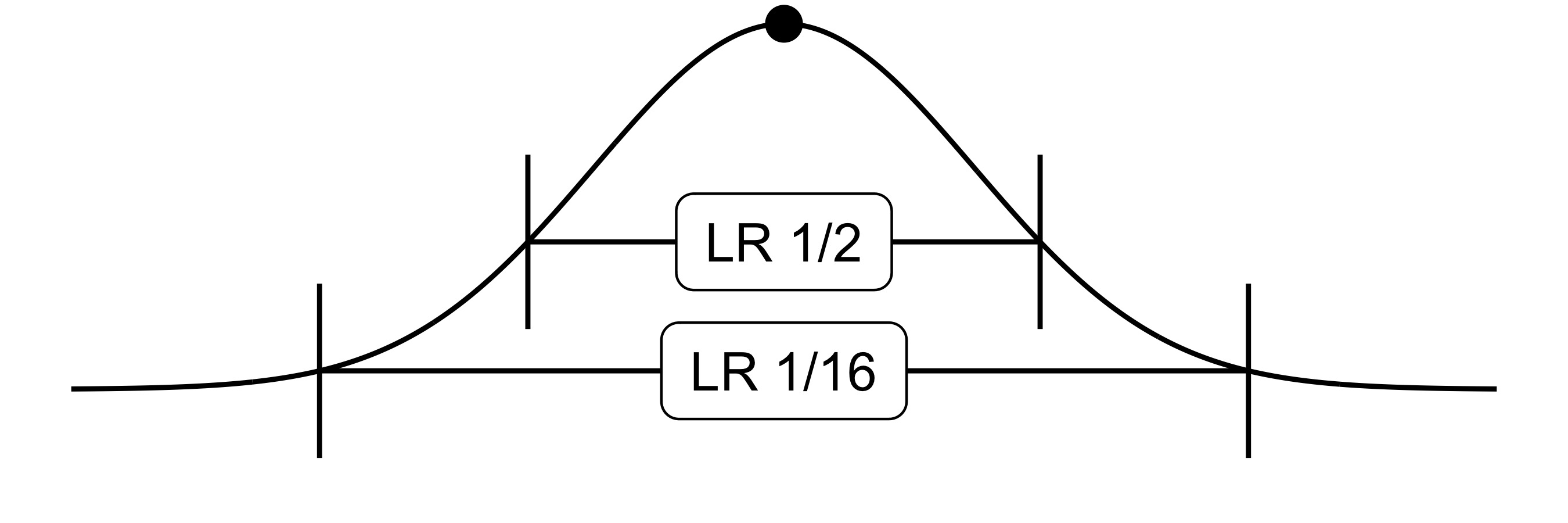
FIGURE 6.2: 1/2 and 1/16 likelihood ratio intervals.
The law of likelihood is stronger than the likelihood principle: The likelihood principle states that the all evidence from the data must be in the likelihood; The law of likelihood describes how evidence can be quantified and compared.
The idea of likelihood ratios lives also in the other statistical modeling mindsets. In frequentism, likelihood ratios are often used as test statistics for hypothesis tests. Likelihood ratio tests are typically used for nested models, where the variables of the first model are a subset of second models variables. Bayesians may use the Bayes factor which compares the ratio of the posterior likelihoods. If both Bayesian models use the same prior probabilities, it’s the same as a likelihood ratio.
But the likelihood ratio has a big problem. While a likelihoodist may interpret it as evidential favoring, the mindset lacks a mechanism to make a definitive answer. Frequentists would use test to decide for one hypothesis or the other. But testing is not allowed for the likelihoodist, or otherwise they would violate the likelihood principle. The likelihood ratio is only an estimate and has some estimation error. How does the modeler know that a ratio of 3 is not just noise, and with a fresh data sample it would be 0.9? Attempts of finding a cut-off lead back to frequentist ideas (which are rejected). Likelihoodism also rejects the idea of Bayesian model interpretation. Bayesian inference estimates posterior probabilities which may be interpreted as updated beliefs about the parameter values and conclusions may be drawn from them. Likelihoodism doesn’t provide the same type of guidance.
6.4 Strengths
- Likelihoodism is a coherent modeling approach: all information is contained in the likelihood. Frequentism, in contrast, is more fragmented with long lists of differently motivated statistical tests and confidence intervals.
- Likelihoodist inference adheres to the likelihood principle.
- Likelihoodism is the most objective of the statistical modeling mindsets. No priors, no imagined experiments.
- Likelihoodist ideas have a home also in Bayesian and frequentist modeling.
6.5 Limitations
- Likelihoodism doesn’t provide guidance in the form of belief or decision. Evidence is less practical.
- To be more specific: There is no good mechanism for deciding if there is enough evidence for one hypothesis.
- Likelihoodism allows only relative statements. It can’t state the probability that a statistical hypothesis is true – only how its evidence compares to another hypothesis.
References
The likelihood principle is violated when data is used to inform the prior. For example, empirical priors which make use of the data violate the likelihood principle.↩︎